Regresión Lineal con NumPy
La regresión lineal se ocupa de investigar la relación entre dos o más variables continuas. En este artículo, veremos cómo obtener una recta de regresión lineal de manera muy sencilla utilizando la librería NumPy, y cómo graficarla junto con los puntos, con la librería matplotlib.
Bienvenidas/os!!, muchas gracias por visitarnos, si están comenzando en Python y este es el primer artículo al que entran en nuestro sitio, les recomendamos visitar Primeros Pasos.
ℹ️ Les recordamos que todos los ejemplos de códigos en nuestro sitio web van a encontrarlos en nuestro repositorio GitHub. Los códigos de este artículo los encontrarán en Linear-Regression_numpy.ipynb.
REGRESIÓN LINEAL
La regresión lineal simple consiste en generar un modelo de regresión, (ecuación de una recta), que permita explicar la relación lineal que existe entre dos variables, una de ellas independiente, y la restante, dependiente.
A la variable independiente o predictora se la conoce como X, mientras que a la variable dependiente o respuesta se la identifica como Y.
El modelo de regresión lineal simple se describe de acuerdo a la ecuación:
$$ Y = \beta_{0} + \beta_{1} x + \epsilon $$
Siendo β0 la ordenada en el origen, β1 la pendiente y ϵ el error aleatorio. Este último representa la diferencia entre el valor ajustado por la recta y el valor real. Recoge el efecto de todas aquellas variables que influyen en Y pero que no se incluyen en el modelo como predictores. Al error aleatorio también se le conoce como residuo.
Una recta de regresión puede emplearse para diferentes propósitos y, dependiendo de ellos, es necesario satisfacer distintas condiciones. En caso de querer medir la relación lineal entre dos variables, la recta de regresión lo va a indicar de forma directa. Sin embargo, en caso de querer predecir el valor de una variable en función de la otra, no sólo se necesita calcular la recta, sino que además hay que asegurar que el modelo sea eficiente. Para ello se utilizan diferentes herramientas, de las cuales mencionaremos:
- R² (Coeficiente de Determinación)
- RMSE (Root Mean Standard Error)
- RSE (Residual Standard Error)
R² (Coeficiente de Determinación)
En los modelos de regresión lineal simple el valor de R² se corresponde con el cuadrado del coeficiente de correlación de Pearson (r) entre X e Y.
R² describe la proporción de variabilidad observada en la variable dependiente explicada por el modelo y relativa a la variabilidad total.
Su valor está acotado entre 0 y 1. (Un valor de R²=1 significa un ajuste lineal perfecto, mientras que un valor de R²=0 indica la no representatividad del modelo lineal). En general, se toman valores de R² entre 0.7-1.0 , (- 0.7 and -1.0), como indicador de una fuerte relación lineal.
RMSE (Root Mean Standard Error)
Una de las formas más sencillas de cuantificar qué tan lejos están los datos de la línea de regresión, es calcular la distancia promedio entre éstos y dicha línea.
Pero, debido a que algunas de las distancias son positivas y otras negativas (ciertos puntos están por encima de la línea de regresión y otros por debajo), estas distancias se cancelarán entre sí, lo que significará una distancia promedio errónea.
Para evitar esta situación, una solución es tomar el cuadrado de esta distancia (que siempre será un número positivo), luego calcular la sumatoria de estas distancias al cuadrado, dividirla por el número de muestras, y finalmente sacar la raíz cuadrada para obtener el Root Mean Standard Error (RMSE).
$$ RMSE = \sqrt{\dfrac{\textstyle\sum_{i=1}^n (Y_{i} - \hat{Y}_{i})^{2}}{n}} $$ donde:
- Yi: valor observado.
- Ŷi: valor pronosticado por el modelo.
- n: número de muestras.
RSE (Residual Standard Error)
Si en lugar de dividir las distancias al cuadrado por el total de muestras n, lo hago por df (degrees of freedom ó grados de libertad), entonces voy a obtener el RSE.
df = n - número de parámetros que quiero estimar.
En general, se utiliza df porque estadísticamente está comprobado que si utilizamos solamente n, vamos a obtener valores muestrales menores a los poblacionales.
$$ RSE = \sqrt{\dfrac{\textstyle\sum_{i=1}^n (Y_{i} - \hat{Y}_{i})^{2}}{df}} $$ donde:
- Yi: valor observado.
- Ŷi: valor pronosticado por el modelo.
- df: número de muestras - parámetros a calcular.
Por ejemplo, si estamos interesados en calcular 3 parámetros (β0, β1, ϵ), como aquí:
$$ Y = \beta_{0} + \beta_{1} x + \epsilon $$
Entonces:
$$ RSE = \sqrt{\dfrac{\textstyle\sum_{i=1}^n (Y_{i} - \hat{Y}_{i})^{2}}{n-3}} $$
ℹ️ Si desean ahondar más en por qué utilizar n-1 en lugar de n, les aconsejamos mirar estos 4 videos de Khan Academy, donde este tema es explicado de una manera muy didáctica, mediante simulaciones matemáticas en lugar de ecuaciones.
REGRESION LINEAL CON NUMPY
Luego de este breve repaso, vamos a continuar con nuestro objetivo de obtener una recta de regresión lineal a partir de la librería NumPy, para luego visualizar los resultados con matplotlib.
Cabe aclarar que, con NumPy sólo calcularemos los valores de m (β1) y b (β0). Si deseamos obtener R², por ejemplo, tendríamos que utilizar otra librería (scikit-learn o scipy lo hacen). En el artículo Regresión Lineal con scikit-learn, explicamos cómo calcular m, b, R², MSE; mientras que en el artículo Regresión Lineal con scipy veremos cómo obtener m, b, R², valor-p.
IMPORTAR LIBRERIAS
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
Como siempre, lo primero que haremos es importar todas las librerías que utilizaremos en el notebook.
CREACIÓN Y VISUALIZACIÓN DE LOS DATOS
Para conseguir una recta de regresión lineal, vamos a necesitar un conjunto de datos. Con este fin, vamos a crear con NumPy 500 pares de puntos (x,y) que sigan una tendencia. Para ello, construiremos una recta con pendiente y ordenada al origen, pero también agregaremos valores aleatorios a cada par de puntos de dicha recta.
# Creamos el conjunto de datos para trabajar
x_data = np.linspace(0.0,10.0,500) # Creamos 500 valores de x equidistantes entre 0 y 10.
np.random.seed(652) # seed obtiene números al azar, pero siempre elegirá los mismos en el mismo orden.
noise = np.random.randn(len(x_data)) # obtengo 500 números aleatorios ya predeterminados por seed.
y_data = (0.5 * x_data ) + 5 + noise # Obtenemos 500 valores de y que seguirán la tendencia de y=0.5x+5
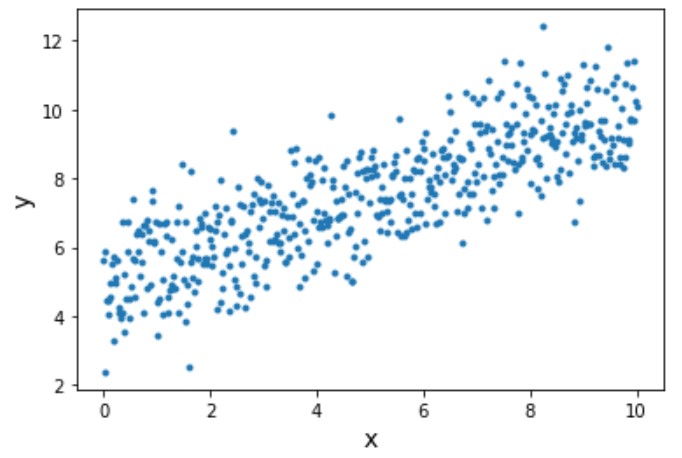
# Graficamos los datos
plt.plot(x_data,y_data,'.')
plt.xlabel('x', fontsize=14)
plt.ylabel('y', fontsize=14)
plt.show()
OBTENCIÓN Y VISUALIZACIÓN DE LA RECTA DE REGRESIÓN LINEAL
linalg.lstsq(A, y, rcond=None)
Esta función calcula los valores de m (β1) y b (β0) utilizando la aproximación por mínimos cuadrados mediante el uso de matrices.
$$ y = mx + b $$
$$ \begin{pmatrix}y\end{pmatrix} = \begin{pmatrix} x \ 1 \end{pmatrix} \begin{pmatrix} m \\ b \end{pmatrix} = Ap $$
$$ A = \begin{pmatrix} x \ 1 \end{pmatrix} \space\space \textnormal{;} \space\space\space p = \begin{pmatrix} m \\ b \end{pmatrix} $$
Creamos la matriz A = (x 1)
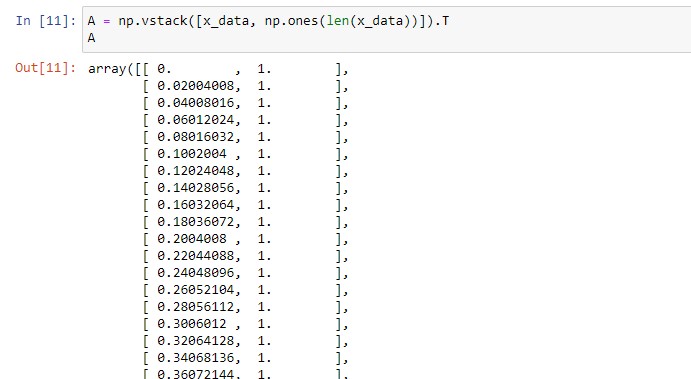
Entonces, para obtener m y b, necesitamos convertir nuestro ndarray x_data al formato de la matriz A = (x 1). Esto lo conseguiremos utilizando np.vstack, el cual va a agregarle al ndarray otra matriz (En este caso, agregaremos una matriz con todos sus elementos con valor 1, y además, la misma cantidad de elementos que x_data). También utilizaremos ndarray.T para obtener la transpuesta de esta nueva matriz.
ℹ️ ndarray es un objeto matriz n-dimensional de NumPy, el cual almacena elementos del mismo tipo.A = np.vstack([x_data, np.ones(len(x_data))]).T
Calculamos “m” y “b”
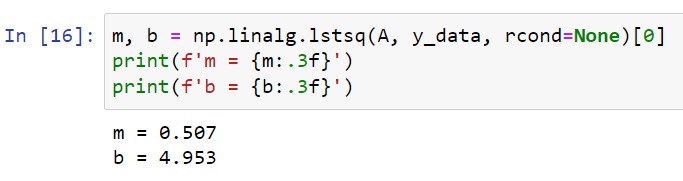
Ahora que tenemos A, podemos calcular m,b utilizando np.linalg.lstsq
m, b = np.linalg.lstsq(A, y_data, rcond=None)[0]
print(f'm = {m:.3f}')
print(f'b = {b:.3f}')
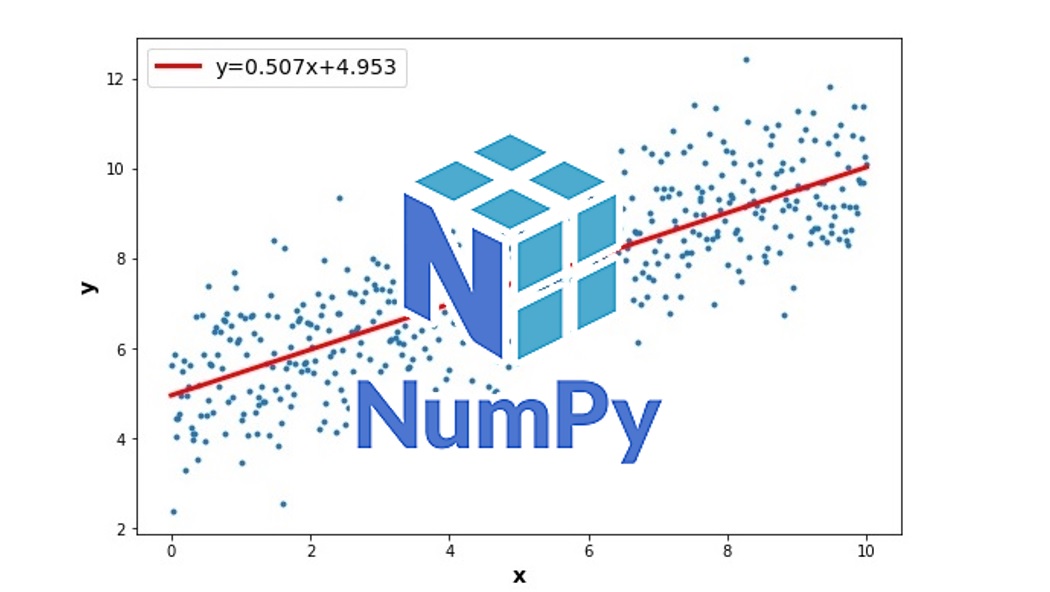
Graficamos los datos originales junto con la recta de regresión lineal
Acto seguido, graficaremos en un mismo plot los datos originales y la recta de regresión lineal obtenida con NumPy.
Para hacerlo más completo, vamos a agregarle al gráfico un label con la ecuación de la recta obtenida.
# Gráfico con los datos originales
plt.figure(figsize=(9, 6))
plt.plot(x_data,y_data,'.')
plt.xlabel('x', fontsize=14,fontweight="bold")
plt.ylabel('y', fontsize=14,fontweight="bold")
# Gráfico recta regresión lineal
plt.plot(x_data, m*x_data + b,'r', linewidth= 3,
label=f'y={m:.3f}x+{b:.3f}')
plt.legend(fontsize=14)
plt.title('DATOS Y RECTA DE REGRESIÓN LINEAL',fontsize=18,fontweight="bold")
plt.show()
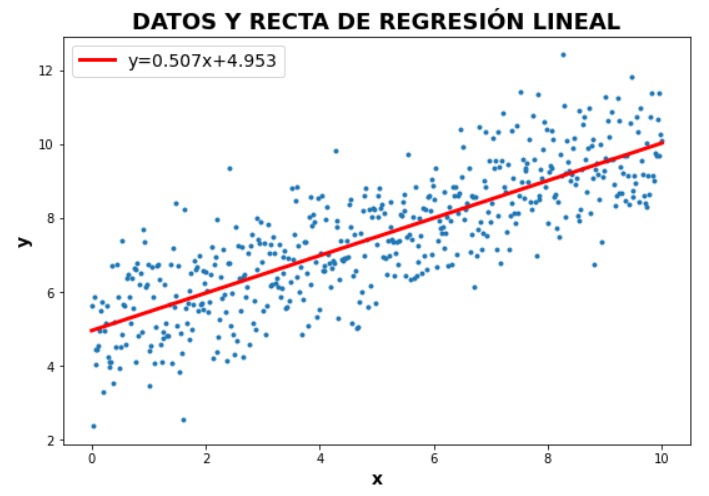
En resumen, creamos un conjunto de datos relacionados entre sí linealmente. Luego calculamos la recta de regresión lineal que mejor los representa utilizando NumPy . Para finalizar, graficamos los datos originales junto con dicha recta con matplotlib.
Les agradecemos su tiempo y esperamos fervientemente que hayan disfrutado este artículo. Si tienen alguna consulta, desean hacer algún comentario o sugerencia para mejorar el contenido, o simplemente indicarles qué les pareció este artículo, debajo pueden hacerlo.
Esperamos reencontrarlos en algún otro artículo del sitio. Hasta luego!
Tags
Recent Posts